티스토리 뷰
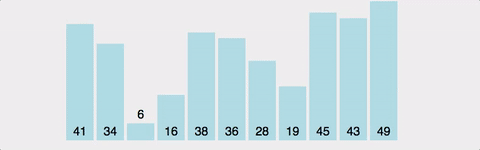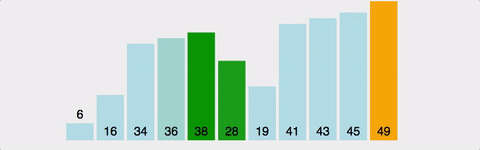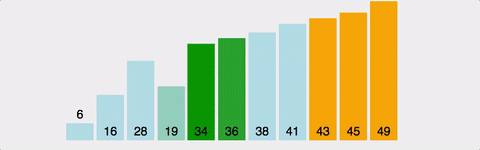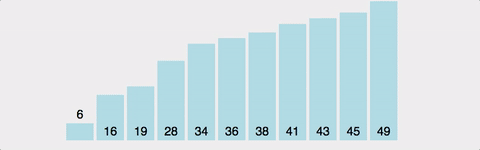
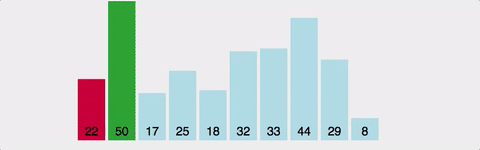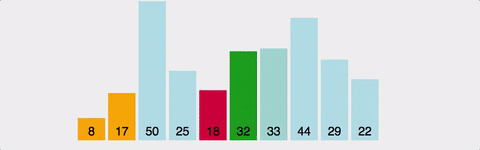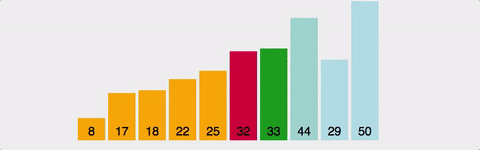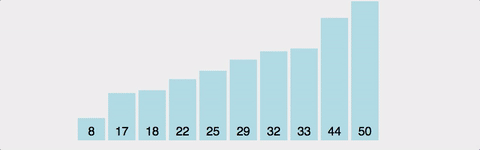
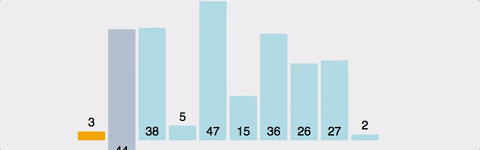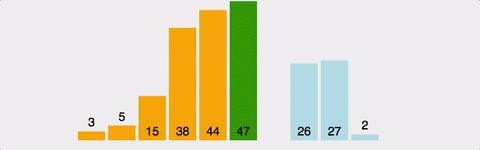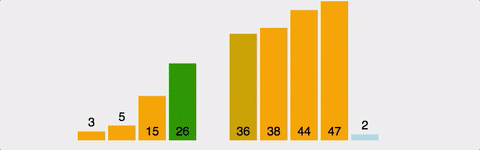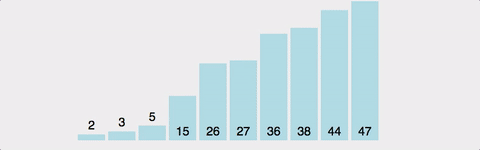
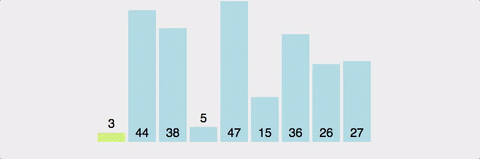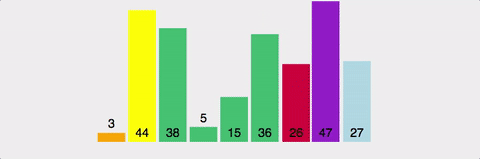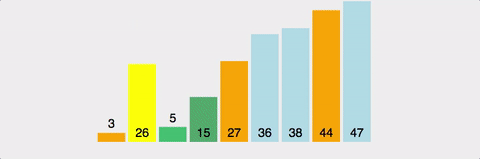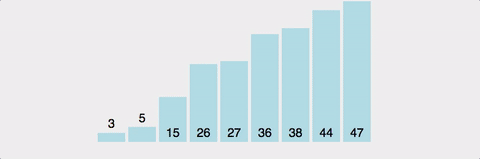
1.버블정렬(Bubble sort)
버블정렬은 가장 쉬운 정렬 알고리즘이지만 시간복잡도가 좋은 퍼포먼스를 내지 못해서 실제로는 잘 사용되지 않는다.
시간복잡도는 O(n²)이며 공간복잡도는 하나의 배열만 사용하여 정렬을 진행하기 때문에 O(n)이다.
버블정렬 소스코드
def bubbleSort(alist):
for loop_count in range(len(alist)-1, 0, -1):
for idx in range(loop_count):
if alist[idx] > alist[idx+1]:
tmp = alist[idx]
alist[idx] = alist[idx+1]
alist[idx+1] = tmp
return alist
버블정렬 테스트결과
각 테스트는 n = 10000으로 진행하였다.
— — Finished! Execution Time 7.72012495995 — -
2. 선택정렬(Selection sort)
선택정렬은 시간복잡도가 O(n²)으로 버블정렬과 정렬하는 알고리즘이 버블정렬과 유사하다. 한번 순회를 하면서 가장 큰 수를 찾아서 배열의 마지막 위치와 교환한다.
선택정렬 소스코드
def selectionSort(alist):
for offset in range(0,len(alist)-1):
offset_minValue = offset
for num in range(offset+1, len(alist)):
if alist[num] < alist[offset_minValue]:
offset_minValue = num
tmp = alist[offset_minValue]
alist[offset_minValue] = alist[offset]
alist[offset] = tmp
return alist
선택정렬 테스트결과(n = 10000)
— — Finished! Execution Time 3.14125704765 — -
3. 삽입정렬(Insertion Sort)
삽입정렬은 1부터 n까지 Index를 설정하여 현재위치보다 아래쪽을 순회하며 현재위치의 값을 현재위치보다 아래쪽으로 순회하며 알맞은 위치에 넣어주는 정렬알고리즘이다.
삽입정렬은 이미 정렬이 되어있다면 O(n)의 시간복잡도를 가지게된다. 정렬이 되어있는 경우라면 한번 순회하며 체크만 하기 때문이며 Big-O 시간복잡도는 O(n²)이다.
삽입정렬 소스코드
def insertionSort(alist):
for index in range(1,len(alist)):
currentvalue = alist[index]
position = index
while position>0 and alist[position-1]>currentvalue:
alist[position]=alist[position-1]
position = position-1
alist[position]=currentvalue
return alist
삽입정렬 테스트결과(n = 10000)
— — Finished! Execution Time 4.19451808929 — -
4. 병합정렬(Merge sort)
병합정렬은 정렬할 리스트를 반으로 쪼개나가며 좌측과 우측 리스트를 계속하여 분할해 나간 후 각 리스트내에서 정렬 후 병합(merge) 정렬 후 병합하는 과정을 통해 정렬하는 알고리즘이다.
병합정렬은 가장 많이 쓰이는 정렬 알고리즘 중 하나 이며 시간복잡도는 최소 O(nlogn)을 보장하게 된다.
병합정렬 소스코드
def mergeSort(alist):
if len(alist) <= 1:
return alist
mid = len(alist) // 2
leftlist = alist[:mid]
rightlist = alist[mid:]
L = mergeSort(leftlist)
R = mergeSort(rightlist)
i = j = 0
result = []
while i < len(L) and j < len(R):
if L[i] < R[j]:
result.append(L[i])
i+=1
else:
result.append(R[j])
j+=1
result += L[i:]
result += R[j:]
return result
병합정렬 테스트결과(n = 10000)
--- Finished! Execution Time 0.0650229454041 ---
else:
tmp = alist[left]
alist[left] = alist[right]
alist[right] = tmp
tmp = alist[start]
alist[start] = alist[right]
alist[right] = tmp
return right
def quickSort(alist, start, end):
if start < end:
pivot = partition(alist, start, end)
quickSort(alist, start, pivot-1)
quickSort(alist, pivot+1, end)
return alist
else:
tmp = alist[left]
alist[left] = alist[right]
alist[right] = tmp
tmp = alist[start]
alist[start] = alist[right]
alist[right] = tmp
return right
if start < end:
pivot = partition(alist, start, end)
quickSort(alist, start, pivot-1)
quickSort(alist, pivot+1, end)
return alist
5. 퀵정렬(Quick sort)
퀵정렬은 real-world 데이터에서 빠르다고 알려져 있어 가장 많이 쓰는 정렬알고리즘이다.
퀵정렬은 pivot을 선정하여 pivot을 기준으로 좌측과 우측으로 pivot보다 작은값은 왼쪽 pivot보다 큰값은 오른쪽으로 재배치를 하고 계속하여 분할하여 정렬하는 알고리즘이다.
최악의 경우에는 O(n²)의 비교를 수행하지만 일반적으로 O(nlogn)의 시간복잡도를 가진다.
퀵정렬 소스코드
def partition(alist, start, end):
pivot = alist[start]
left = start+1
right = end
done = False
while not done:
while left <= right and alist[left] <= pivot:
left += 1
while alist[right] >= pivot and right >= left:
right -= 1
if right < left:
done = True
else:
tmp = alist[left]
alist[left] = alist[right]
alist[right] = tmp
tmp = alist[start]
alist[start] = alist[right]
alist[right] = tmp
return right
def quickSort(alist, start, end):
if start < end:
pivot = partition(alist, start, end)
quickSort(alist, start, pivot-1)
quickSort(alist, pivot+1, end)
return alist
퀵정렬 테스트결과(n = 10000)
6. 힙정렬(Heap sort)
 | |
| 분류 | 정렬 알고리즘 |
|---|---|
| 자료 구조 | 배열 |
| 최악 시간복잡도 | |
| 최선 시간복잡도 | |
| 평균 시간복잡도 | |
| 공간복잡도 | |
힙 정렬(Heapsort)이란 최대 힙 트리나 최소 힙 트리를 구성해 정렬을 하는 방법으로서, 내림차순 정렬을 위해서는 최대 힙을 구성하고 오름차순 정렬을 위해서는 최소 힙을 구성하면 된다. 최대 힙을 구성하여 정렬하는 방법은 아래 예와 같다.
- n개의 노드에 대한 완전 이진 트리를 구성한다. 이때 루트 노드부터 부노드, 왼쪽 자노드, 오른쪽 자노드 순으로 구성한다.
- 최대 힙을 구성한다. 최대 힙이란 부노드가 자노드보다 큰 트리를 말하는데, 단말 노드를 자노드로 가진 부노드부터 구성하며 아래부터 루트까지 올라오며 순차적으로 만들어 갈 수 있다.
- 가장 큰 수(루트에 위치)를 가장 작은 수와 교환한다.
- 2와 3을 반복한다.
'Algorithm' 카테고리의 다른 글
| 이진검색 - drying (0) | 2018.07.30 |
|---|